ГЛОБАЛЬНАЯ ОПТИМИЗАЦИЯ:… > Тестовые задачи глобальной…

Тестовые задачи глобальной оптимизации с ограничениями

G2 problem

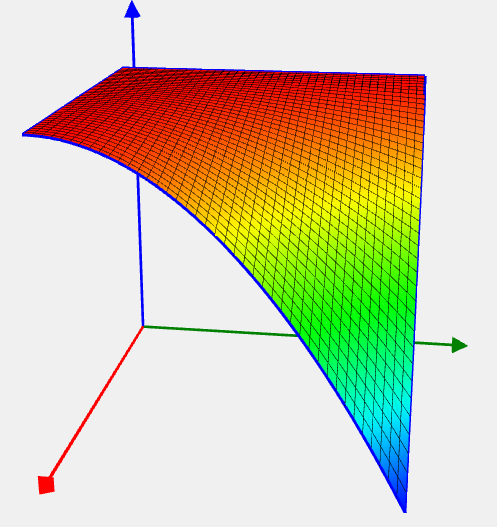Целевая функция

$f(x) = - \bigl| \frac{\sum_{i=1}^n\cos^4 (x_i) - 2 \prod_{i=1}^n \cos^2(x_i)}{\sqrt{\sum_{i=1}^n i x_i^2}}\bigr|.$

Ограничения

$0.75 - \prod_{i=1}^n x_i \leq 0,$

$\sum_{i=1}^n x_i - 7.5n \leq 0.$

Характеристики

Размерность: $n = 20$ .
Область поиска: $0 \leq x_i \leq 10$ , $1 \leq i \leq n$ .
Глобальный минимум: неизвестен, наилучшее решение $f(x^\star) = -0.803619$ .
Источники: [3, 4]

G8 problem

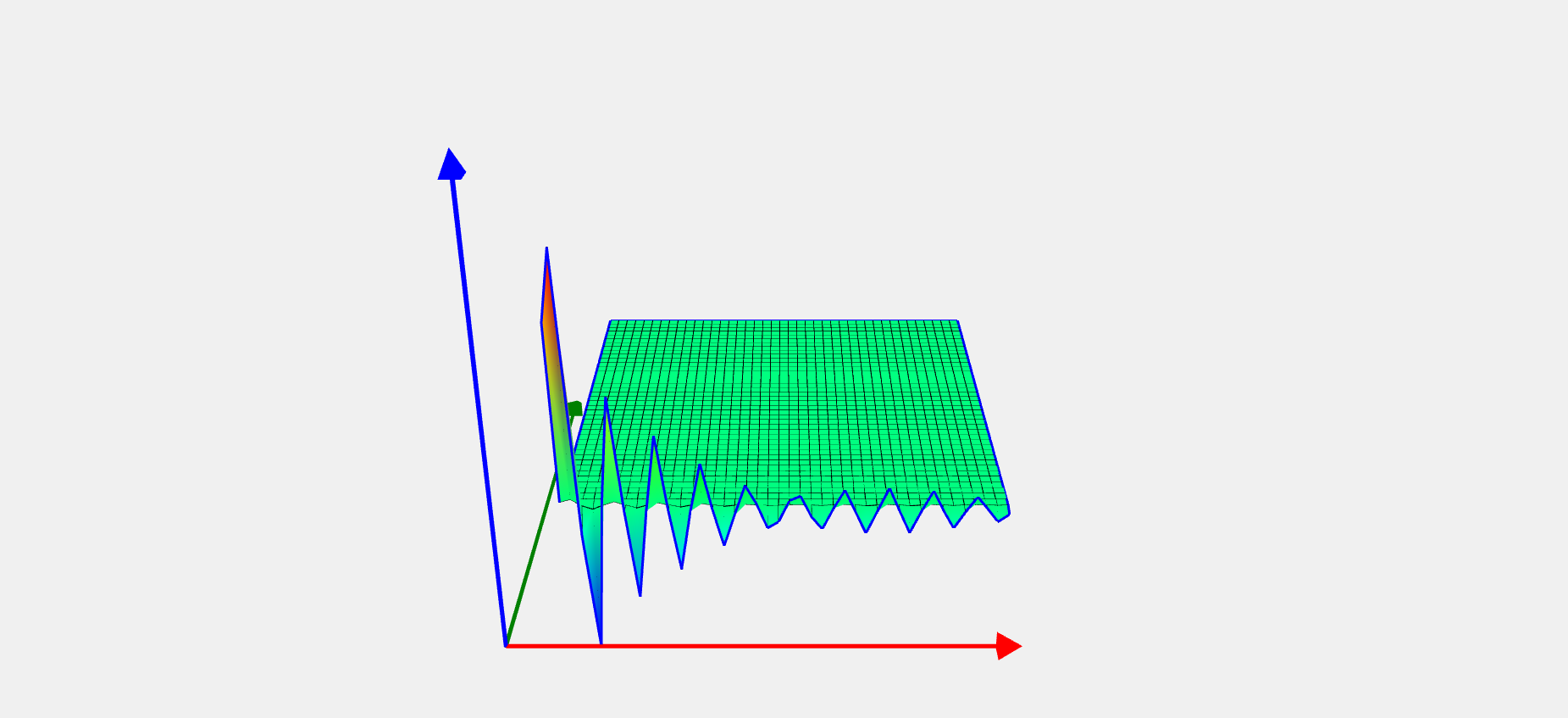Целевая функция

$f(x) = - \frac{\sin^3(2\pi x_1) \sin(2\pi x_2)}{x_1^3(x_1+x_2)}.$

Ограничения

$x_1^2 - x_2 + 1 \leq 0,$

$1 - x_1 + (x_2 - 4)^2 \leq 0.$

Характеристики

Размерность: $n = 2$ .
Область поиска: $0 \leq x_i \leq 10$ , $i = 1, 2$ .
Глобальный минимум: $f(1.2279713, 4.2453733) = -0.095825$ .
Источники: [3, 4]

Kim problem

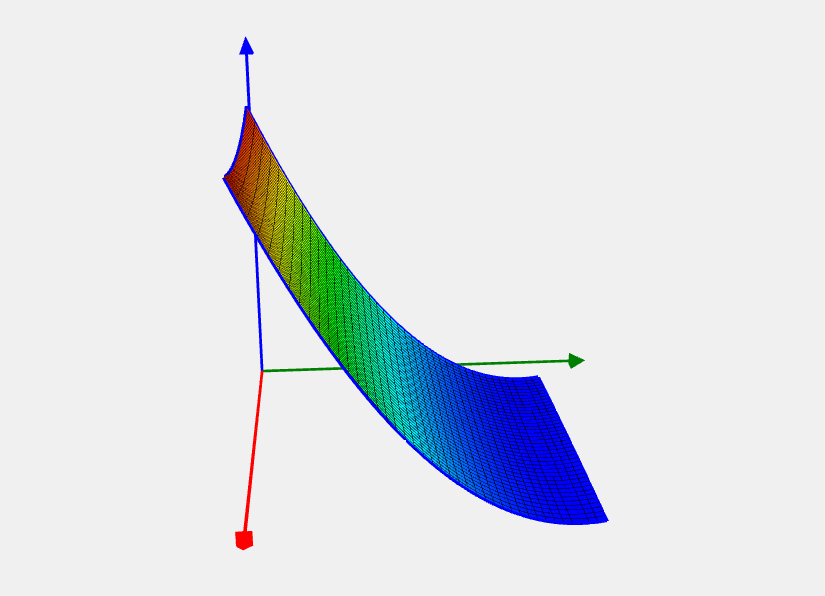Целевая функция

$f(x) = 100(x_2 - x_1^2)^2 + (1 - x_1)^2.$

Ограничения

$- x_1 - x_2^2 \leq 0,$

$-x_1^2 - x_2 \leq 0.$

Характеристики

Размерность: $n = 2$ .
Область поиска: $-0.5 \leq x_1 \leq 0.5$ , $-10 \leq x_2 \leq 1$ .
Глобальный минимум: $f(0.5, 0.25) = 0.25$ .
Источники: [5]

Madsen problem

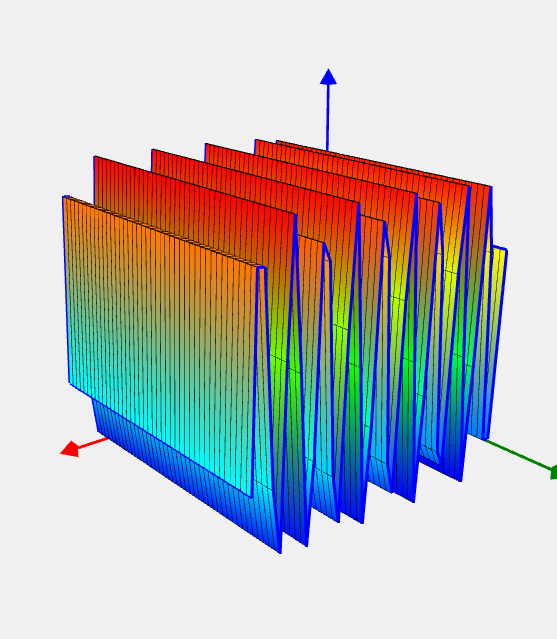Целевая функция

$f(x) = x_3.$

Ограничения

$- \cos x_2 + x_3 \leq 0,$

$x_1^2 + x_2^2 + x_1 x_2 - x_3 \leq 0,$

$-\sin x_1 - x_3 \leq 0,$

$- (x_3 + x_1^2 + x_2^2 + x_1 x_2) \leq 0,$

$\sin x_1 - x_3 \leq 0.$

Характеристики

Размерность: $n = 3$ .
Область поиска: $-100 \leq x_i \leq 100$ , $i = 1, 2, 3$ .
Глобальный минимум: $f(0.453275,-0.906592, 0.616432) = 0.616432$ .
Источники: [1]

Mishra’s bird problem

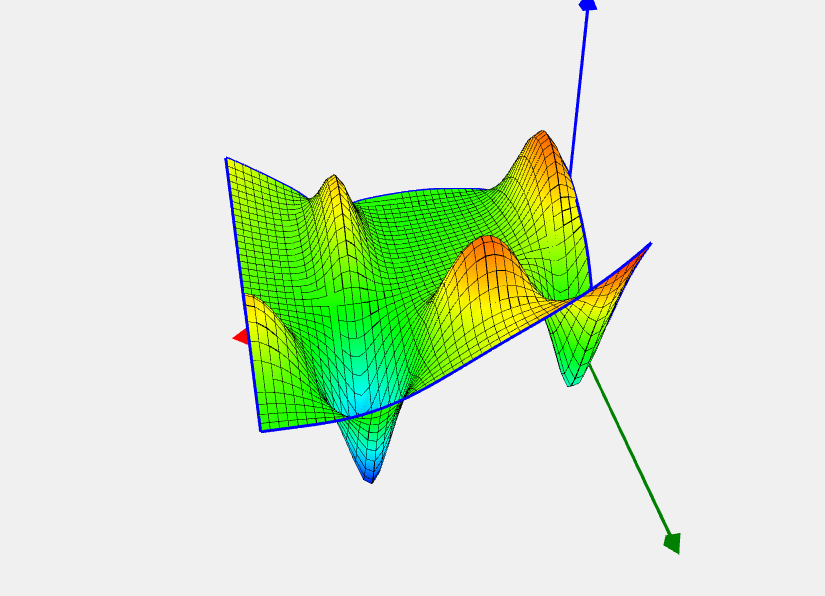Целевая функция

$f(x) = \sin(x_2) \exp{[(1 - \cos x_1)^2]} + \cos (x_1) \exp{[(1 - \sin x_2)^2]} + (x_1 - x_2)^2.$

Ограничения

$(x_1 + 5)^2 + (x_2 + 5)^2 - 25 < 0.$

Характеристики

Размерность: $n = 2$ .
Область поиска: $-10 \leq x_1 \leq 0$ , $-6.5 \leq x_2 \leq 0$ .
Глобальный минимум: $f(-3.1302468, -1.5821422) = -106.7645367$ .
Источники: […]

Romeijn 1 problem

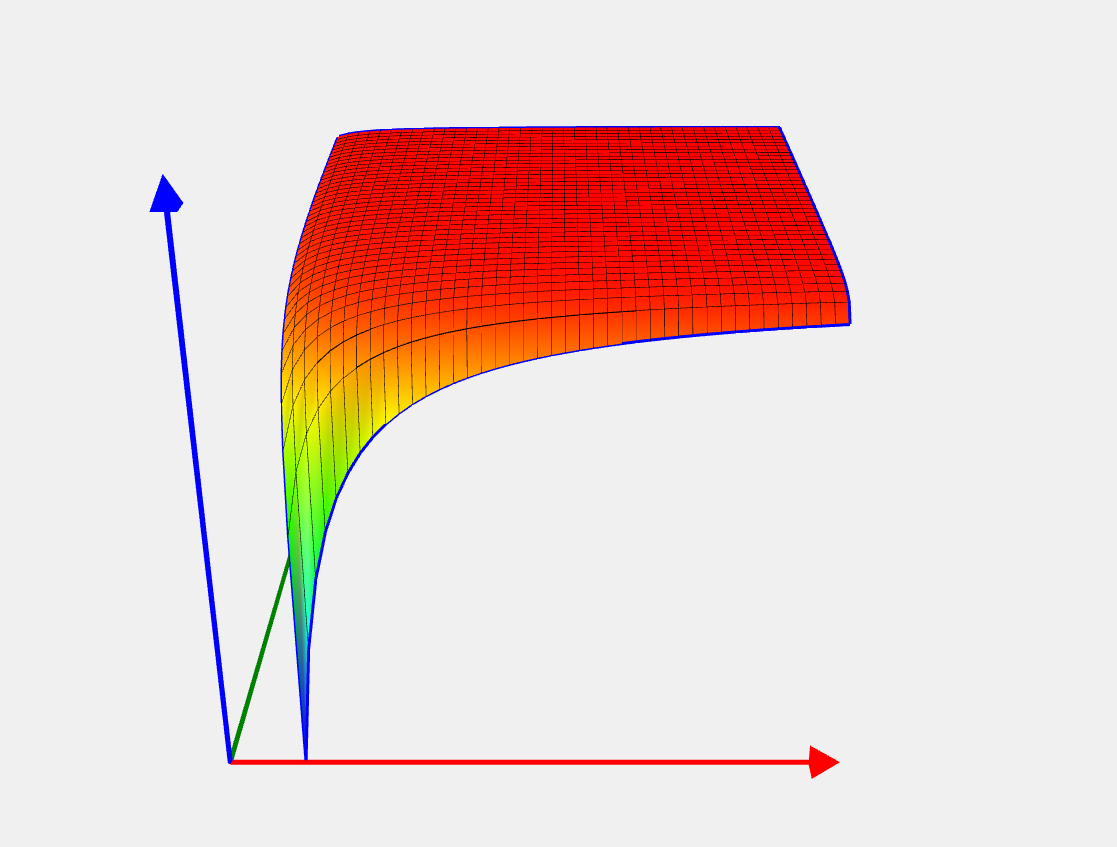Целевая функция

$f(x) = - \frac 1 {x_1^2 x_2 x_3}.$

Ограничения

$\begin{gather*} 0.44098 x_1 + 28.46 x_1^2 + 6158.4 x_1^2 x_2 + 0.0037018 x_3 + 5.4474 x_3^2 + 0.032236 x_1 x_3 \\ + 2.92 x_2 x_3 + 0.44712 x_2 + 37.964 x_2^2 + 42.876 x_1 x_2 - 1 \leq 0. \end{gather*}$

Характеристики

Размерность: $n = 3$ .
Область поиска: $0 \leq x_1 \leq 0.18745$ , $0 \leq x_2 \leq 0.16230$ , $0 \leq x_3 \leq 0.42846$ .
Глобальный минимум: неизвестен.
Источники: [2]

Romeijn 2 problem

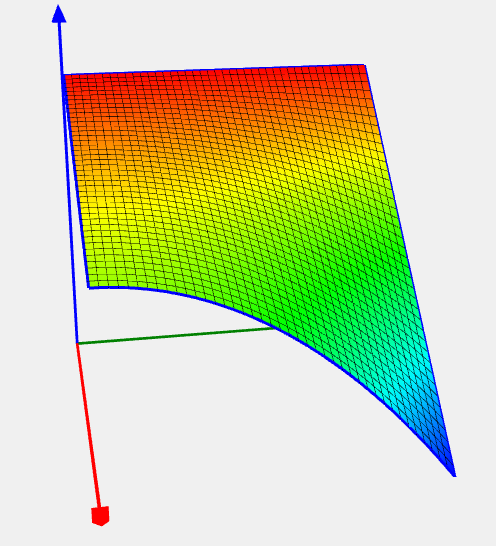Целевая функция

$f(x) = - (0.0204 + 0.0607x_5^2) x_1 x_4 (x_1 + x_2 + x_3) - (0.0187 + 0.0437x_6^2) x_2 x_3 (x_1 + 1.57x_2 + x_4),$

Ограничения

$\frac{2070}{x_1 x_2 x_3 x_4 x_5 x_6} - 1 \leq 0,$

$0.00062 x_1 x_4 x_5^2 (x_1 + x_2 + x_3) + 0.00058 x_2 x_3 x_6^2 (x_1 + 1.57 x_2 + x_4) - 1 \leq 0.$

Характеристики

Размерность: $n = 6$ .
Область поиска: $0 \leq x_1 \leq 10$ , $0 \leq x_2 \leq 10$ , $0 \leq x_3 \leq 15$ , $0 \leq x_4 \leq 15$ , $0 \leq x_5 \leq 1$ , $0 \leq x_6 \leq 1$ .
Глобальный минимум: $f(10, 10, 15, 4.609, 0.78511, 0.3814) = -316.27$ .
Источники: [1, 2]

Romeijn 3 Problem

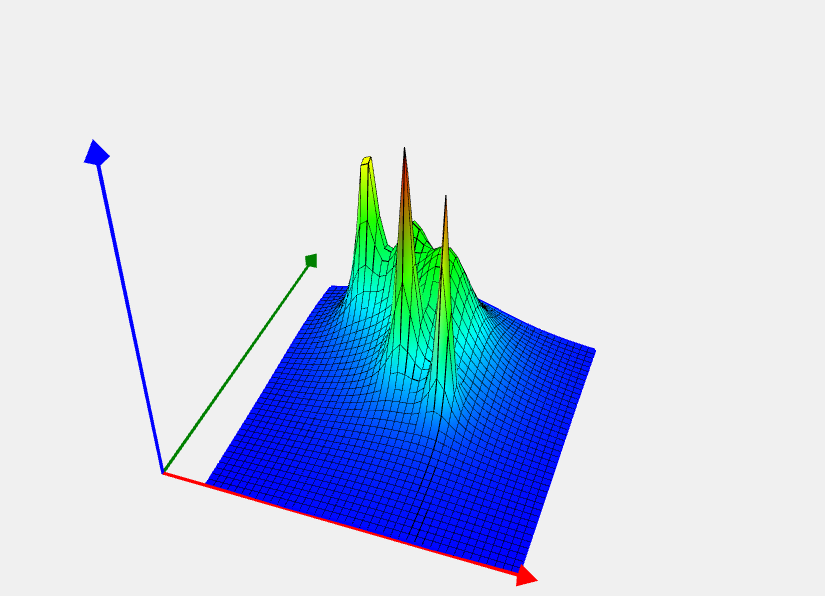Целевая функция

$f(x) = \sum_{i=1}^5 \frac 1 {a_i(x-p_i)^\intercal (x-p_i) + c_i}.$

Ограничения

$x_1 + x_2 \leq 5,$

$x_1 - x_2^2 \leq 0,$

$5x_1^3 - \frac 8 5 x_2^2 \leq 0,$

где величины $a_{i}$ , $p_i$ и $c_i$ приведены в Таблице 1.

Характеристики

Размерность: $n = 2$ .
Область поиска: $-3 \leq x_1 \leq 10$ , $-4 \leq x_2 \leq 7$ .
Глобальный минимум: $f(-3, -4) = 0.18301$ .
Источники: [1, 2]

Таблица 1. Данные для задачи Romeijn 3 Problem

$i$	$a_i$	$p_i$	$c_i$
1	0.5	(0, 5)	0.125
2	0.25	(2, 5)	0.25
3	1	(3, 2)	0.1
4	1/12	(4, 4)	0.2
5	2	(5, 1)	1/12

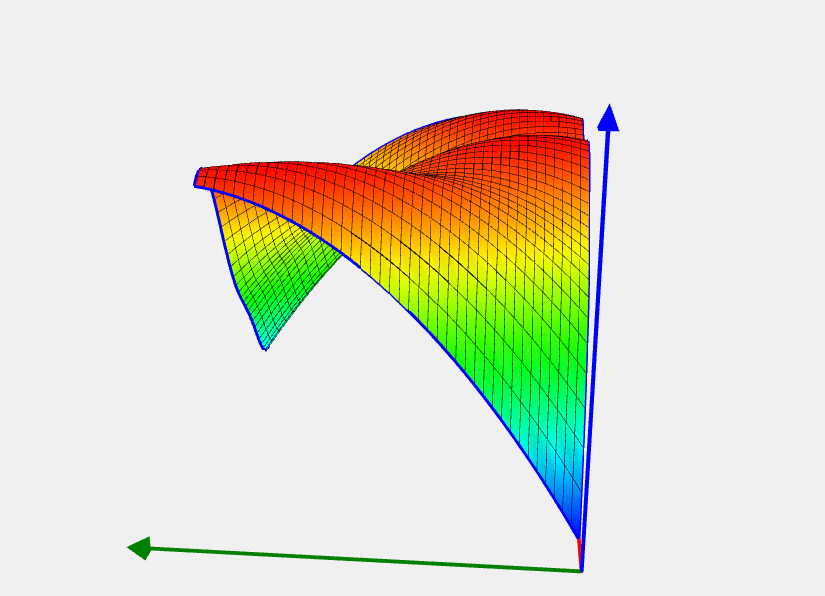
Romeijn 5 problem

Целевая функция

$f(x) = -(x_2 - 1.275x_1^2 + 5x_1 - 6)^2 - 10(1-\frac 1 {8\pi}) \cos(\pi x_1) - 10.$

Ограничения

$-\pi x_1 - x_2 \leq 0,$

$- \pi^2 x_1^2 + 4 x_2 \leq 0.$

Характеристики

Размерность: $n = 2$ .
Область поиска: $-\frac 3 2 \leq x_1 \leq \frac 7 2$ , $0 \leq x_2 \leq 15$ .
Глобальный минимум: $f(2.4656, 15) = -195.37$ .
Источники: [1, 2]

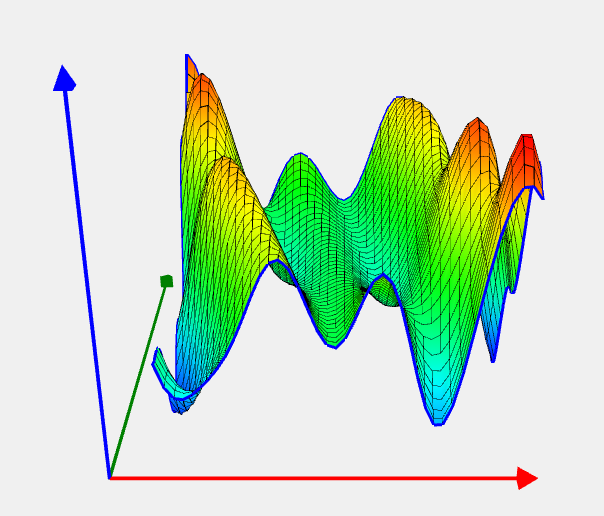
Townsend problem

Целевая функция

$f(x) = -\cos^2((x_1 - 0.1)x_2) - x_1 \sin(3x_1 + x_2).$

Ограничения

$x_1^2 + x_2^2 - [2\cos t - \frac 1 2 \cos 2t - \frac 1 4 \cos 3t - \frac 1 8 \cos 4t]^2 - (2 \sin t)^2 < 0,$

$t = Atan2(x_1, x_2).$

Характеристики

Размерность: $n = 2$ .
Область поиска: $-2.25 \leq x_1 \leq 2.5$ , $-2.5 \leq x_2 \leq 1.75$ .
Глобальный минимум: $f(2.0052938, 1.1944509) = -2.0239884$ .
Источники: […]

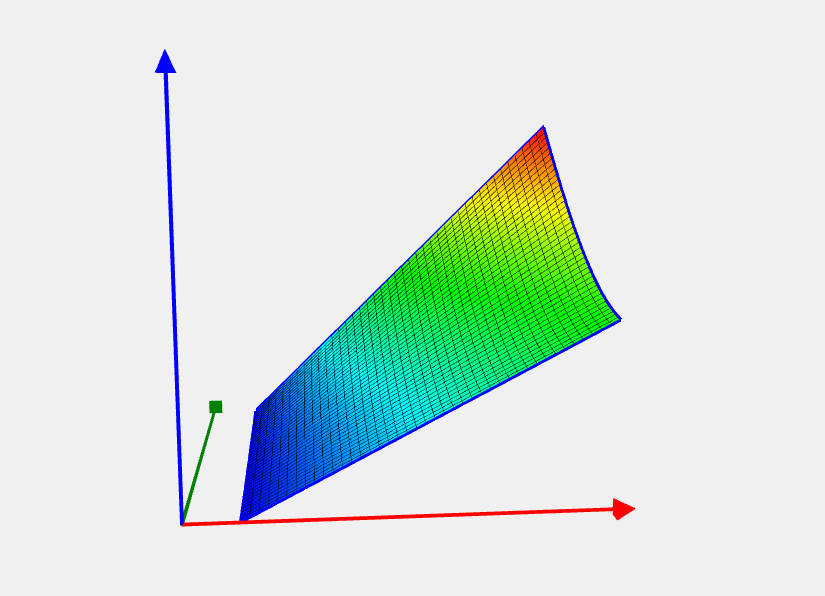
Two Bars problem

Целевая функция

$f(x) = x_1 \sqrt{1 + x_2^2},$

Ограничения

$0.124\sqrt{1+x_2^2} \times (\frac 8 {x_1} + \frac 1 {x_1 x_2}) - 1 \leq 0,$

$0.124\sqrt{1+x_2^2} \times (\frac 8 {x_1} - \frac 1 {x_1 x_2}) - 1 \leq 0.$

Характеристики

Размерность: $n = 2$ .
Область поиска: $0.2 \leq x_1 \leq 4$ , $0.1 \leq x_2 \leq 1.6$ .
Глобальный минимум: $f(1.41163, 0.377072) = 1.5087$ .
Источники: [1]

Использованные источники

Z. Kajee-Bagdadi. Differential Evolution Algorithms for Constrained Global Optimization. Johannesburg /not an article/.
H. E. Romeijn, R. L. Smith. Simulated Annealing for Constrained Global Optimization. Journal of Global
Optimization, 1994, V. 5, Issue 2, pp. 101–126.
E. Mezura-Montes, C.A.C. Coello. A Simple Multimembered Evolution Strategy to Solve Constrained
Optimization Problems. IEEE Transactions on Evolutionary Computation, V. 9, No.1, pp. 1-17, 2005.
Z. Michalewicz, M. Schoenauer. Evolutionary Algorithms for Constrained Parameter Optimization Problems.
Evolutionary Computation. V. 4, No. 1, pp. 1-32, 1996.
J.H. Kim, H. Myung. Evolutionary Programming Techniques for Constrained Optimization Problems. IEEE
Transactions on Evolutionary Computation, V. 1, No. 2, 1997.