Ключевые особенности подхода
Основным результатом является информационно-статистическая теория для построения методов глобально глобального поиска. Методы, разработанные в рамках информационно-статистической теории, основаны на вероятностных представлениях о возможном поведении многоэкстремальной целевой функции и применимы для решения широкого класса задач.
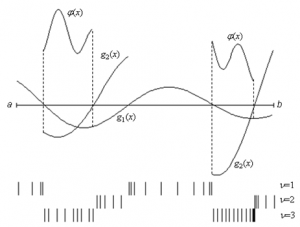 Задача с частично определенными функциями |
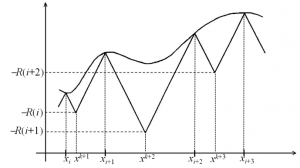 Построение липшицевой миноранты функции |
Например, для решения задач с невыпуклыми ограничениями (в рамках информационно-статистического подхода) был разработан оригинальный способ учета ограничений (индексный метод). Характерной чертой этого подхода, не использующего идей метода штрафных функций, является раздельный учет каждого ограничения задачи. В соответствии с правилами индексного метода каждая итерация, называемая также испытанием в соответствующей точке области поиска, включает последовательную проверку выполнимости ограничений задачи в этой точке, а обнаружение первого нарушенного ограничения прерывает испытание и инициирует переход к точке следующей итерации.
Алгоритмы, разработанные в рамках информационно-статистического подхода, основаны на предположении липшицевости всех функционалов задачи. Предположение такого рода является достаточно естественным для многих прикладных задач, поскольку относительные вариации функционалов, характеризующих моделируемую систему, обычно не могут превышать некоторый порог, определяемый ограниченной энергией изменений в системе. Также допускается, что некоторые функционалы задачи определены не во всей области поиска. Это обстоятельство может быть важным в приложениях, поскольку невыполнение некоторых (представленных ограничениями) условий для одних характеристик задачи может вызвать неопределенность других характеристик.
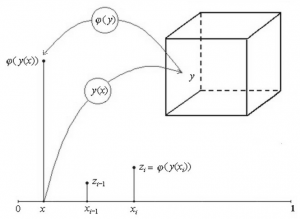 Схема редукции размерности |
 Кривая, заполняющая пространство |
Для решения многомерных задач разработана не имеющая аналогов схема редукции размерности, в рамках которой решение многомерной задачи сводится к решению эквивалентного ей набора одномерных задач. Соответствующая редукция основана на использовании разверток единичного отрезка вещественной оси на гиперкуб. Роль таких разверток играют непрерывные однозначные отображения типа кривой Пеано, называемые также кривыми, заполняющими пространство, и их обобщения, названные «множественными развертками». Указанный тип отображений позволяет организовать параллельное решение нескольких информационно-связанных эквивалентных друг другу задач. При этом решение любой из них будет одновременно являться решением исходной задачи.
Для организации параллельных вычислений была разработана общая схема, учитывающая принципиальные особенности современных суперкомпьютерных систем. Так, для вычислительных узлов с распределенной памятью предлагается использовать методы распараллеливания с использованием множественных разверток, для вычислительных узлов с общей памятью будет применяться распараллеливание на основе интервальных характеристик подобластей поиска. В данной схеме предусмотрена возможность использования графических процессоров и ускорителей Intel Xeon Phi.

