Ackley’s Problem
|
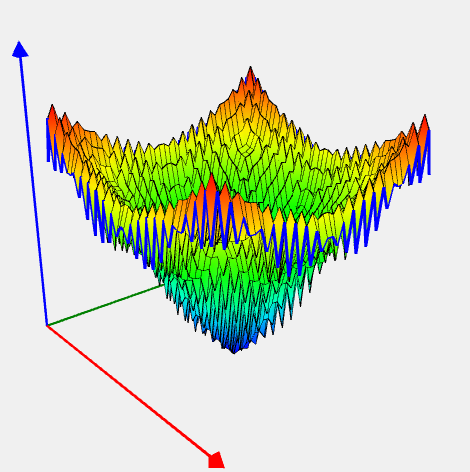 |
![Rendered by QuickLaTeX.com \[ f(x) = -20 \exp(-0.02 \sqrt{\frac{\sum_{i=1}^n x_i^2}{n}}) - \exp(\frac{\sum_{i=1}^n \cos(2 \pi x_i)}{n}) + 20 + e. \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-bccba191de5159c9eb07d5363c3cac20_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов: неизвестно.
- Источники: [1, 2, 4, 5, 6, 7, 10, 11, 13, 14, 15]
|
Camel Back — 3 (Three Hump) Problem
|
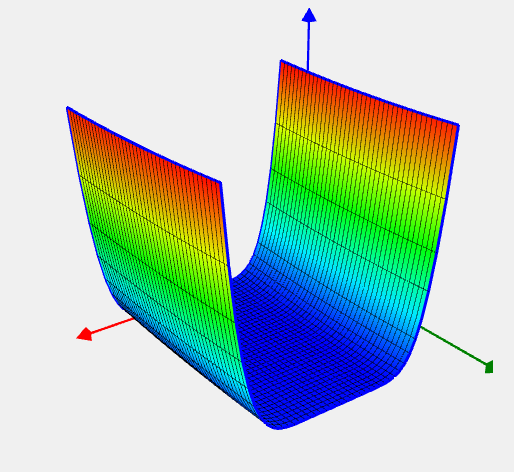 |
![Rendered by QuickLaTeX.com \[ f(x) = 2 x_1^2 - 1.05x_1^4 + \frac 1 6 x_1^6 +x_1 x_2 + x_2^2. \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-6b712cf09cc6bf5e27edf1b1a723bc13_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 4, 9, 10, 11, 12, 13, 14, 16]
|
Camel Back — 6 (Six Hump) Problem
|
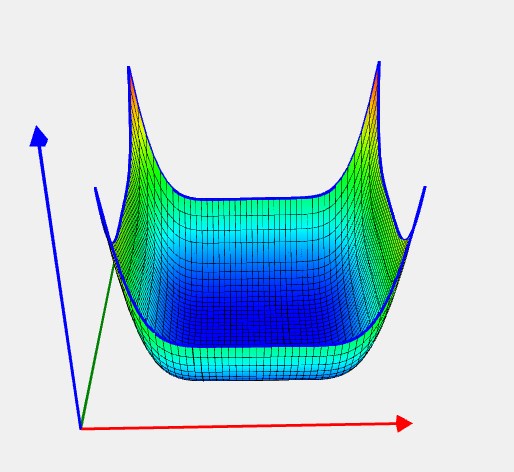 |
![Rendered by QuickLaTeX.com \[ f(x) = 4 x_1^2 - 2.1 x_1^4 + \frac 1 3 x_1^6 + x_1 x_2 - 4 x_2^2 + 4 x_2^4. \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-2a495b9098576fd02833b283e9fb01b3_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 2, 4, 6, 7, 9, 10, 12, 13, 14, 16]
|
Griewank Problem
|
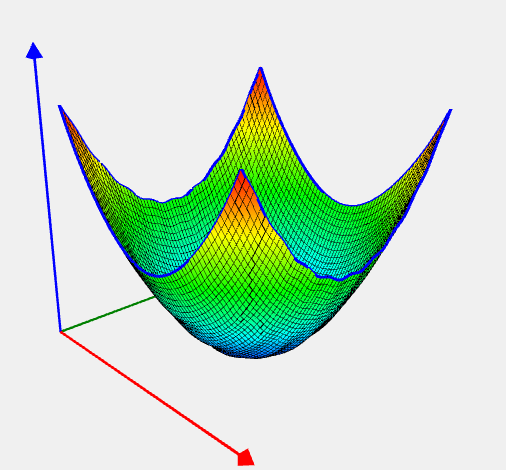 |
![Rendered by QuickLaTeX.com \[ f(x) = 1 + \frac 1 {4000}\sum_{i=1}^n x_1^2 - \prod_{i=1}^{n} \cos(\frac{x_i}{\sqrt{i}}). \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-b75214fadc7e9bab7170f7100e9432fa_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов: неизвестно; при
 около около  . .
- Источники: [1, 2, 4, 5, 6, 7, 10, 11, 13, 14, 16]
|
Levy and Montavlo 1 Problem
|
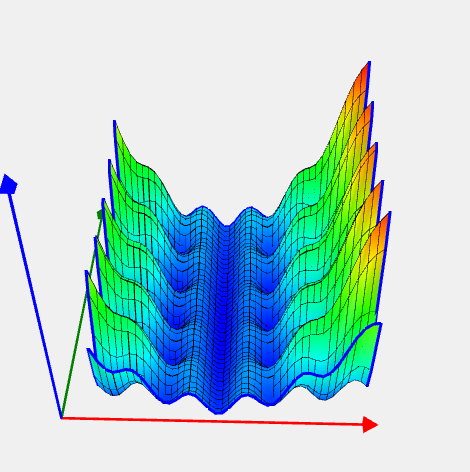 |
![Rendered by QuickLaTeX.com \[ f(x) = \frac{\pi}{n}\Bigl(10\sin^2(\pi y_1) + \sum_{i=1}^{n-1}(y_i-1)^2[1+10\sin^2(\pi y_{i+1})] + (y_n-1)^2\Bigr), \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-6453aeeee114a4c7f980b27d56b07f5e_l3.svg)
где  . . |
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 10, 13, 14, 15]
|
McCormick Problem
|
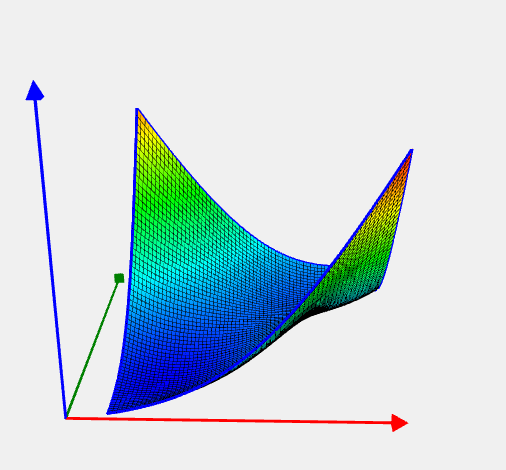 |
![Rendered by QuickLaTeX.com \[ f(x) = \sin(x_1+x_2) + (x_1-x_2)^2 - \frac 3 2 x_1 + \frac 5 2 x_2 + 1. \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-fd0d25ed1538c45bc2e2af7456241663_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 4, 10, 13, 14]
|
Modified Langerman Problem
|
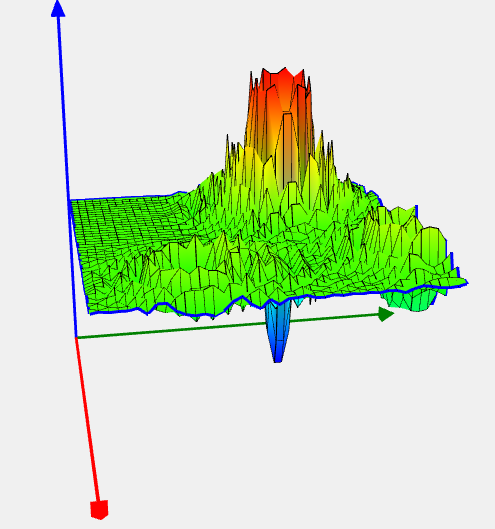 |
![Rendered by QuickLaTeX.com \[ f(x) = - \sum_{j=1}^{5}c_j \cos(\frac{d_j}{\pi})\exp(-\pi d_j), \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-a8cf7a1081bd0447417543acccd9f7c1_l3.svg)
где  и значения и значения  и и  приведены в Таблице 1. приведены в Таблице 1. |
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
- Количество локальных минимумов: неизвестно.
- Источники: [1, 4, 9, 10]
|
Таблица 1. Данные для задачи Modified Langerman Problem
 |
 |
 |
 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
0.806 |
9.681 |
0.667 |
4.783 |
9.095 |
3.517 |
9.325 |
6.544 |
0.211 |
5.122 |
2.020 |
| 2 |
0.517 |
9.400 |
2.041 |
3.788 |
7.931 |
2.882 |
2.672 |
3.568 |
1.284 |
7.033 |
7.374 |
| 3 |
0.100 |
8.025 |
9.152 |
5.114 |
7.621 |
4.564 |
4.711 |
2.996 |
6.126 |
0.734 |
4.982 |
| 4 |
0.908 |
2.196 |
0.415 |
5.649 |
6.979 |
9.510 |
9.166 |
6.304 |
6.054 |
9.377 |
1.426 |
| 5 |
0.965 |
8.074 |
8.777 |
3.467 |
1.867 |
6.708 |
6.349 |
4.534 |
0.276 |
7.633 |
1.567 |
|
Neumaier 2 Problem
|
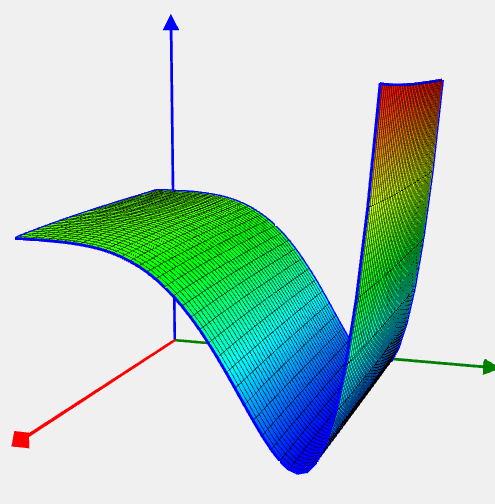 |
![Rendered by QuickLaTeX.com \[ f(x) = \sum_{k=1}^{n}\Bigl(b_k - \sum_{i=1}^n x_i^k\Bigr)^2, \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-60891a4a9f27970a9cb78e141f9cccf0_l3.svg)
где  . . |
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов: неизвестно.
- Источники: [1, 10, 13, 14, 15, 16]
|
Neumaier 3 Problem
|
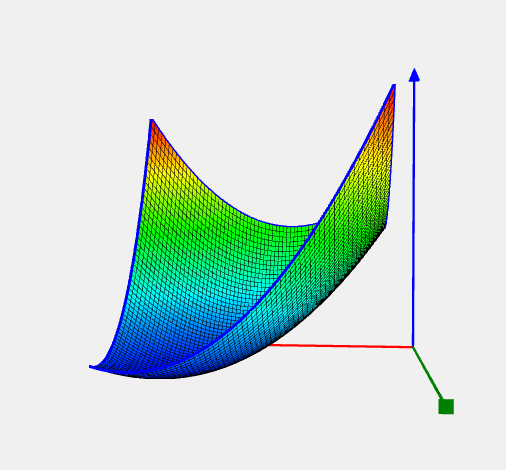 |
![Rendered by QuickLaTeX.com \[ f(x) = \sum_{i=1}^{n}(x_i-1)^2 - \sum_{i=2}^n x_i x_{i-1}. \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-fccb66b038fa30d60146b695fb68039e_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 , ,  . .
- Количество локальных минимумов: неизвестно.
- Источники: [1, 10, 13, 16]
|
Paviani Problem
|
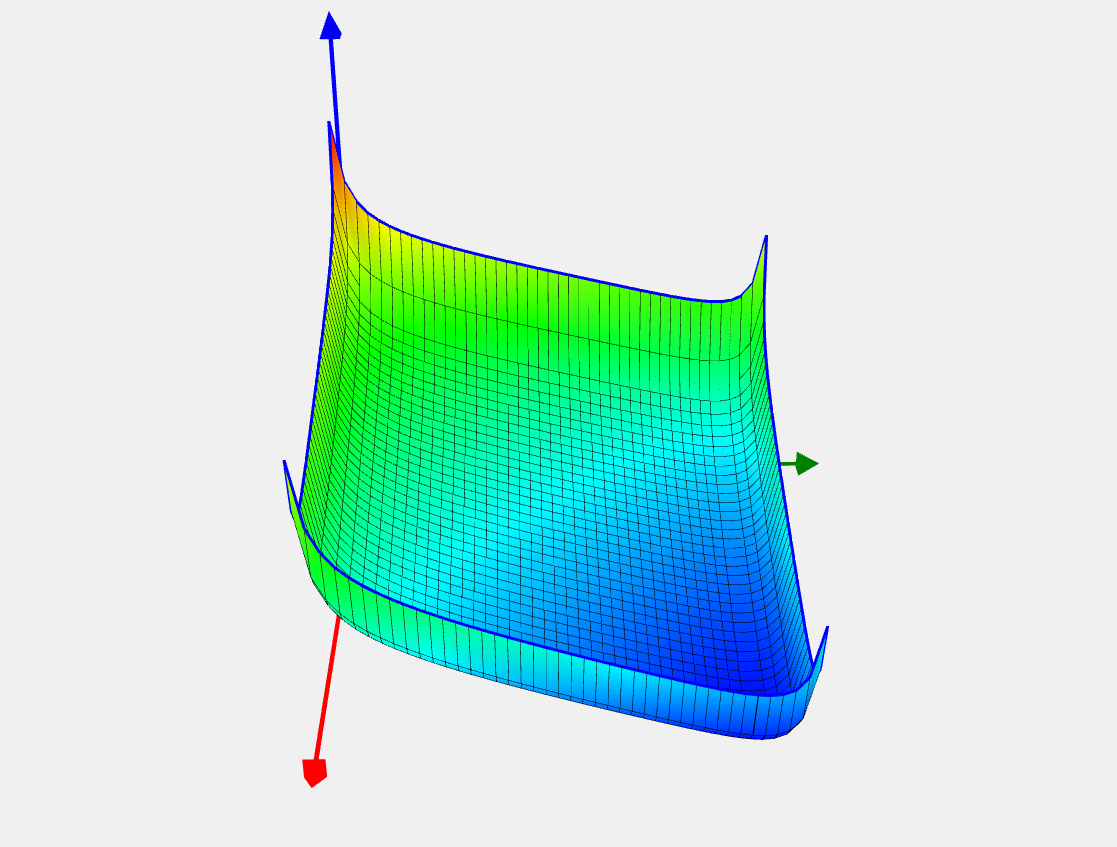 |
![Rendered by QuickLaTeX.com \[ f(x) = \sum_{i=1}^{10}[\ln^2(x_i-2) + \ln^2(10-x_i)] - (\prod_{i=1}^{10}x_i)^{0.2}. \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-39b76b02e4522a9ac78b2ce428900fb3_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 , ,  . .
- Количество локальных минимумов: неизвестно.
- Источники: [1, 4, 10, 12, 13, 14]
|
Rosenbrock Problem
|
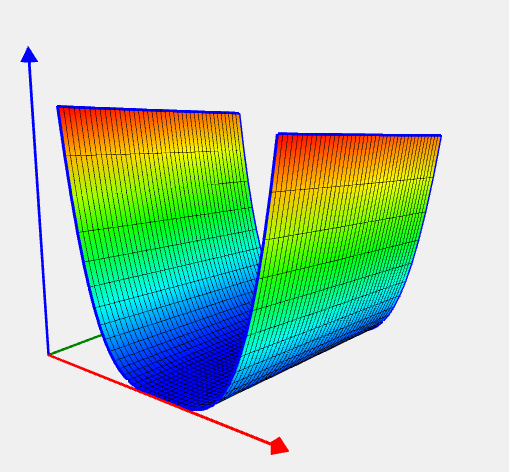 |
![Rendered by QuickLaTeX.com \[ f(x) = \sum_{i=1}^{n-1}\Bigl(100(x_{i+1}-x_i^2)^2 + (x_i-1)^2\Bigr). \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-41597e273f2d7e49498b8444017ffe3c_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 16]
|
Salomon Problem
|
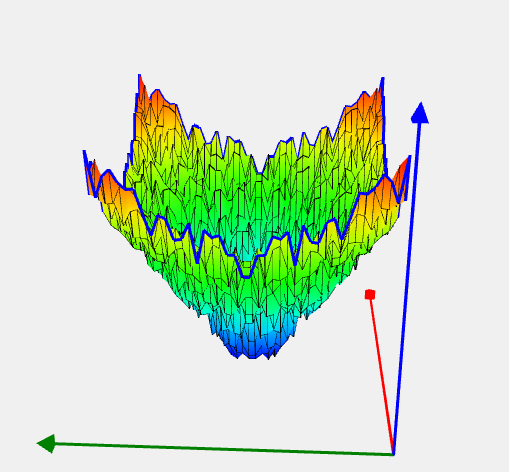 |
![Rendered by QuickLaTeX.com \[ f(x) = 1 - \cos(2\pi \|x\|) + 0.1 \|x\|, \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-43cb37a72778887252f4f3023ec01ad3_l3.svg)
где  . . |
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 , ,  . .
- Количество локальных минимумов: неизвестно.
- Источники: [1, 4, 10, 11, 12, 13, 14]
|
Schwefel Problem
|
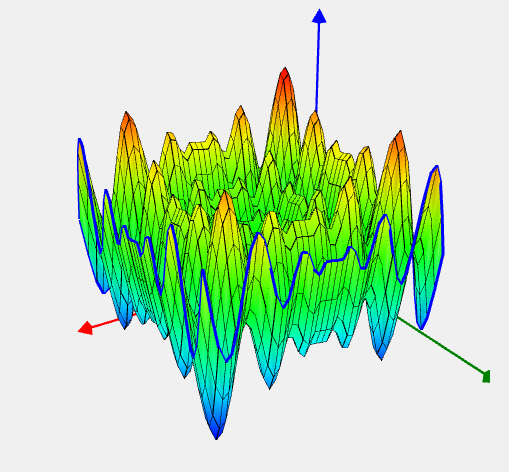 |
![Rendered by QuickLaTeX.com \[ f(x) = - \sum_{i=1}^n x_i \sin(\sqrt{|x_i|}). \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-99a9502e8848cea8b3ff2249fcd61ff9_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 , где , где  . .
- Количество локальных минимумов: неизвестно.
- Источники: [1, 2, 4, 5, 7, 10, 12]
|
Shekel 5 Problem
|
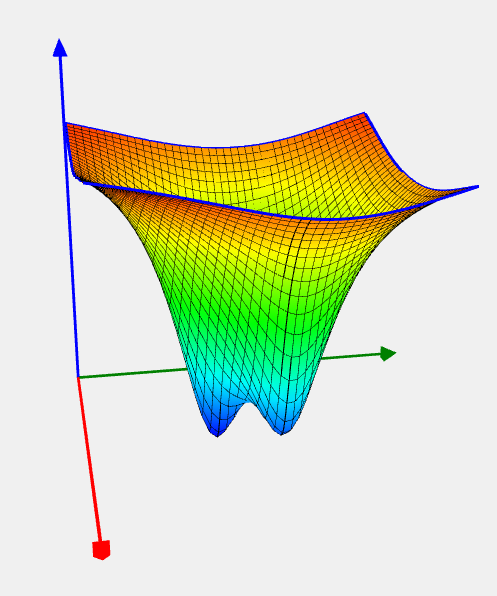 |
![Rendered by QuickLaTeX.com \[ f(x) = - \sum_{i=1}^{5}\frac{1}{\sum_{j=1}^4(x_j-a_{ij})^2+c_i}, \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-947db5d0abd27eb4af47f40b1d79640e_l3.svg)
где величины  и и  приведены в Таблице 2. приведены в Таблице 2. |
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 2, 4, 6, 8, 10, 12, 13, 14, 16]
|
Таблица 2. Данные для задач Shekel Problems
 |
 |
 |
 |
 |
 |
 |
| 1 |
4 |
4 |
4 |
4 |
0.1 |
| 2 |
1 |
1 |
1 |
1 |
0.2 |
| 3 |
8 |
8 |
8 |
8 |
0.2 |
| 4 |
6 |
6 |
6 |
6 |
0.4 |
| 5 |
3 |
7 |
3 |
7 |
0.4 |
| 6 |
2 |
9 |
2 |
9 |
0.6 |
| 7 |
5 |
5 |
3 |
3 |
0.3 |
| 8 |
8 |
1 |
8 |
1 |
0.7 |
| 9 |
6 |
2 |
6 |
2 |
0.5 |
| 10 |
7 |
3.6 |
7 |
3.6 |
0.5 |
|
Shekel 7 Problem
|
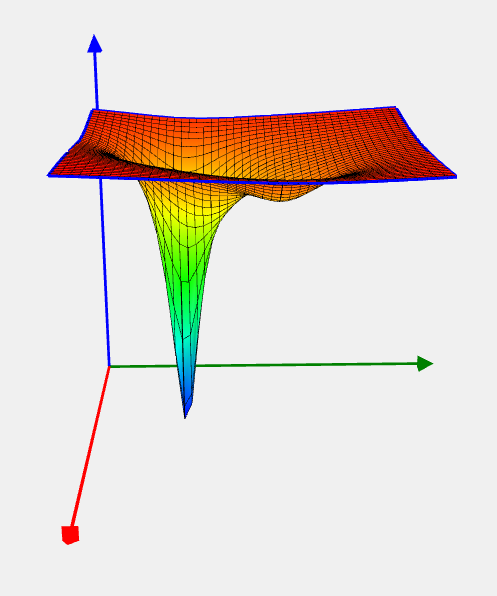 |
![Rendered by QuickLaTeX.com \[ f(x) = - \sum_{i=1}^{7}\frac{1}{\sum_{j=1}^4(x_j-a_{ij})^2+c_i}, \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-e843a46f6ae00eed11232a3abb5a5ce1_l3.svg)
где величины  и и  приведены в Таблице 2. приведены в Таблице 2. |
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 2, 4, 6, 8, 10, 12, 13, 14, 16]
|
Shekel 10 Problem
|
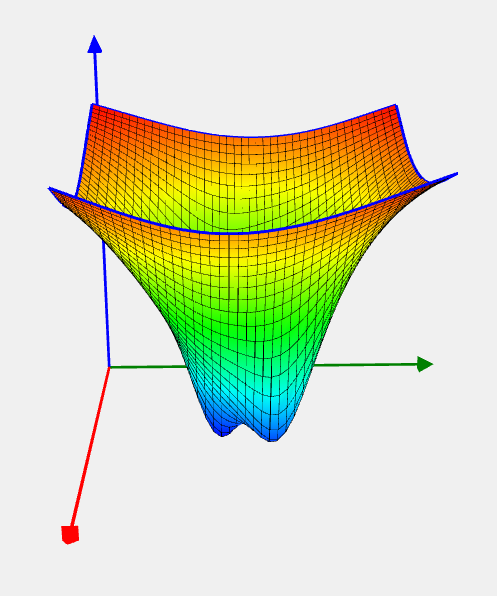 |
![Rendered by QuickLaTeX.com \[ f(x) = - \sum_{i=1}^{10}\frac{1}{\sum_{j=1}^4(x_j-a_{ij})^2+c_i}, \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-70b2eb8b74b9f809ea70720b520b2435_l3.svg)
где величины  и и  приведены в Таблице 2. приведены в Таблице 2. |
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум:
 . .
- Количество локальных минимумов:
 . .
- Источники: [1, 2, 4, 6, 8, 10, 12, 13, 14, 16]
|
Shubert Problem
|
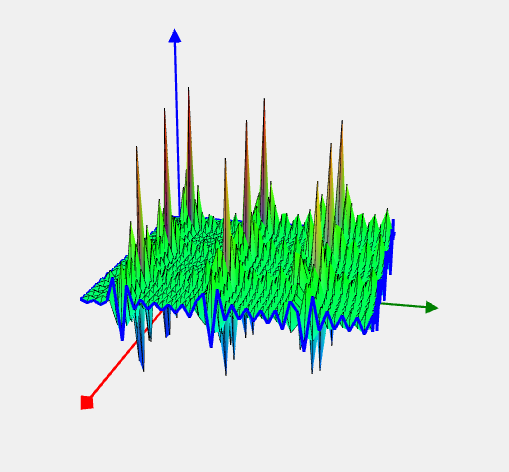 |
![Rendered by QuickLaTeX.com \[ f(x) = \prod_{i=1}^n(\sum_{j=1}^5 j \cos((j+1)x_i + j)). \]](https://hpc-education.unn.ru/wp-content/ql-cache/quicklatex.com-ee9dd3364062df5810d0f2a241d911df_l3.svg)
|
- Размерность:
 . .
- Область поиска:
 , ,  . .
- Глобальный минимум: 18 точек глобального минимума,
 . .
- Точки глобального минимума приведены в Таблице 3.
- Количество локальных минимумов:
 . .
- Источники: [1, 2, 4, 6, 8, 10, 12, 13]
|
Таблица 3. Точки глобального минимума для задачи Shubert Problem
| (-7.0835, 4.8580) |
(-7.0835, -7.7083) |
(-1.4251, -7.0835) |
(5.4828, 4.8580) |
(-1.4251, -0.8003) |
(4.8580, 5.4828) |
| (-7.7083, -7.0835) |
(-7.0835, -1.4251) |
(-7.7083, -0.8003) |
(-7.7083, 5.4828) |
(-0.8003, -7.7083) |
(-0.8003, -1.4251) |
| (-0.8003, 4.8580) |
(-1.4251, 5.4828) |
(5.4828, -7.7083) |
(4.8580, -7.0835) |
(5.4828, -1.4251) |
(4.8580, -0.8003) |
|
Использованные источники
|
- M.M. Ali, C. Khompatraporn, Z.B. Zabinsky. A numerical evaluation of several stochastic algorithms on selected continuous global optimization test problems. Journal of Global Optimization, 31(4), 635-672. (2005)
- M. Laguna, R. Marti. Experimental Testing of Advanced Scatter Search Designs for Global Optimization of Multimodal Functions, Journal of Global Optimization, V. 33, 235-255. (2005)
- H.E. Romeijn, R.L. Smith. Simulated annealing for constrained global optimization. Journal of Global Optimization 5(2): 101-126. (1994)
- M. Jamil and X.S. Yang. A literature survey of benchmark functions for global optimization problems, Int. Journal of Mathematical Modelling and Numerical Optimization, Vol. 4, №2, 150-194. (2013)
- J. Teo. Global Optimization Accuracy and Evolutionary Dynamics of the Generalized Generation Gap Algorithm with Adaptive Mutation. Malaysian Journal of Computer Science, 19(2): 159-167. (2006)
- Q. Tao, X. Huang, S. Wang, L. Li. Adaptive block coordinate DIRECT algorithm. Journal of Global Optimization. 69:4, 797-822. (2017)
- X.S. Yang. Test Problems in Optimization. Engineering Optimization: An Introduction with Metaheuristic Applications, John Wiley & Sons. (2010)
- R. Paulavicius, J. Zilinskas, A. Grothey. Investigation of selection strategies in branch and bound algorithm with simplicial partitions and combination of Lipschitz bounds. Optimization Letters, 4:173-183. (2010)
- Z. Nedelkova, P. Lindroth, M. Patriksson, A.B. Stromberg. Efficient solution of many instances of a simulation-based optimization problem utilizing a partition of the decision space. Annals of Operation Research, 1-26. (2017)
- K. M. Mullen. Continuous Global Optimization in R. Journal of Statistical Software, 60:6, 1-45. (2014)
- N.S. Teng, M.H.A. Hijazi and J. Teo. Self-adaptive Scaling Factor in Differential Evolution. Regional Conference on Computational Science and Technologies (RCCST 2007), 112-116. (2007)
- Y. Alipouri, J. Poshtan, H. Alipouri. Improvement of Classical Evolutionary Programming using State Feedback Controller. Int. J. of Innovative Computing, Information and Control, Vol.10, № 4, 1413-1433. (2014)
- N. Henderson, M. Sa Rego, W.F. Sacco, R.A. Rodrigues. A new look at the topographical global optimization method and its application to the phase stability analysis of mixtures. Chemical Engineering Science. 127: 151-174. (2015)
- F. Shahzad, S. Masood, N. K. Khan. Probabilistic opposition-based particle swarm optimization with velocity clamping, Knowledge and Information Systems, Vol. 39, Issue 3, 703-737. (2014)
- Q. Abbas, J. Ahmad, H. Jabeen. A novel tournament selection based differential evolution variant for continuous optimization problems. Mathematical Problems in Engineering, Article ID 205709, 21pp. (2015)
- L. G. Casado, I. Garcia, T. Csendes, V.G. Ruiz. Heuristic Rejection in Interval Global Optimization. Journal of Optimization Theory and Applications, Vol. 118, №1, 27-43. (2003)
|


















