Область исследований
Областью исследований являются вычислительно-трудоемкие задачи Глобальной Оптимизации.
Ключевые особенности исследуемых задач:
- Существенная многоэкстремальность оптимизируемых функций (возможность наличия значительного количества локально-оптимальных вариантов в области поиска).
- Наличие сложных нелинейных ограничений, которые могут порождать невыпуклые и многосвязные области допустимых решений. Данные ограничения могут быть частично-вычислимыми, когда нарушение хотя бы одного ограничения приводит к невозможности вычисления всех остальных функционалов задачи.
- Высокая вычислительная сложность (значения критериев и ограничений могут определяться в результате длительных вычислений для сложных математических моделей изучаемых явлений и систем).
- Возможная многокритериальность, когда при выборе оптимальных решений должны учитываться несколько различных показателей эффективности. Постановка задачи может динамично варьироваться в ходе вычислений в результате изменения состава имеющихся критериев и ограничений.
Задачи глобальной оптимизации рассмотренного класса имеют общий характер и широко распространены в приложениях (оптимальное проектирование, идентификация параметров и др.). Решение подобных задач является проблемой огромной вычислительной сложности и может быть обеспечено только с помощью высокоэффективных параллельных алгоритмов глобальной оптимизации при использовании высокого вычислительного потенциала современных суперкомпьютерных систем.
Иллюстративный пример задачи глобальной оптимизации
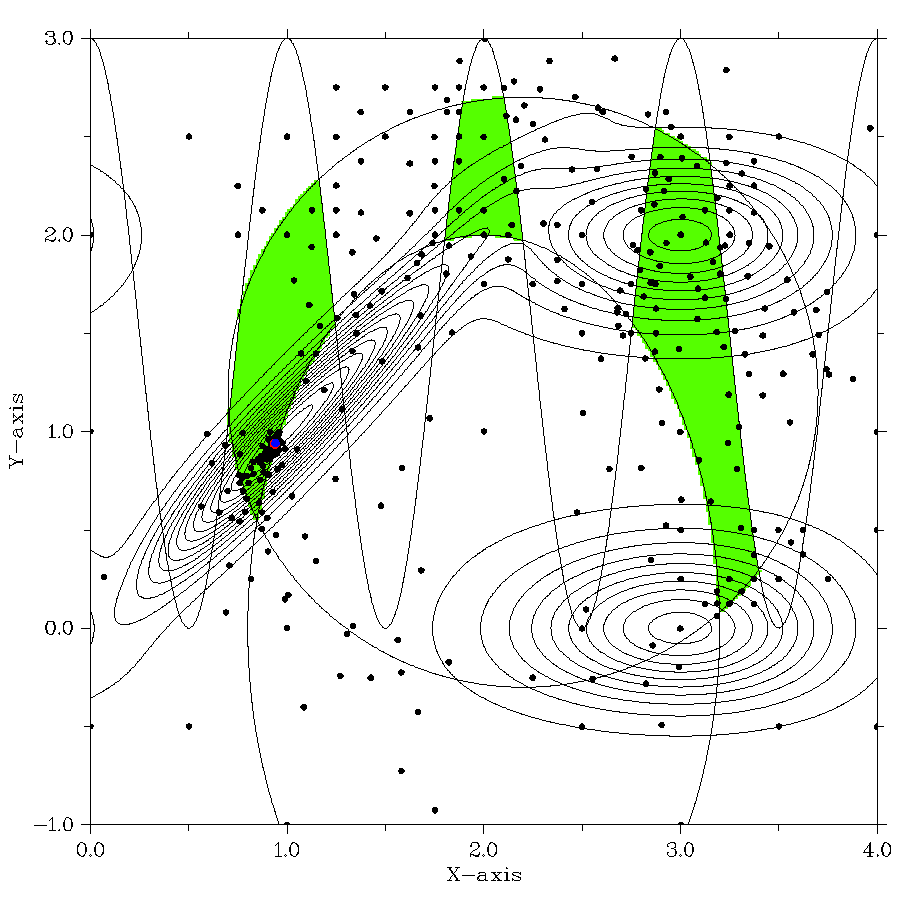
На рисунке показан пример двумерной задачи глобальной оптимизации, в которой имеется три ограничения. Допустимая область поиска, состоящая из трех подобластей, выделена зеленым цветом. На рисунке показаны линии уровня оптимизируемой (целевой) функции. Всего в области поиска имеется три локальных минимума. Расположение глобального минимума выделено точкой синего цвета. Точки, в которых вычислялись значения целевой функции и ограничений, показаны черным цветом. Как следует из приведенных результатов, применяемый алгоритм глобального поиска сходится только к точке глобального минимума.

